這篇主要是參考李教授的影片,以及網路上的文章,整理的筆記。
Algorithm 1: Training

第 1 行:repeat
- 作用: 開始一個迭代訓練過程,直到模型收斂
第 2 行
- 作用: 從數據分佈 中取一個樣本 (x0)(即從訓練數據集中抽取一個數據點)。
- x0 代表 clean Image。
- q(x0): 數據分佈,即訓練集中數據的真實分佈。
第 3 行
- 作用: 隨機選擇一個時間t。
第 4 行
- 作用: 取一個隨機噪聲樣本 。
- 解釋:
- 擴散過程中,數據會逐步被加上噪聲,最終變成完全隨機的高斯噪聲。
- 在訓練過程中,需要用隨機噪聲模擬這個擴散過程。
- 解釋:
第 5 行:梯度下降更新
∇_θ ‖ε − ε_θ(√ᾱ_t x_0 + √(1−ᾱ_t) ε, t)‖²
- 細節解釋:
ε 為原始噪聲
ε_θ(√ᾱ_t x_0 + √(1−ᾱ_t) ε, t) 這一段做的則是 noise predictor。
而 noise predictor 會有以下兩個 input
input 1. √ᾱ_t x_0 + √(1−ᾱ_t) ε ; input 2. t 代表第幾個回合的 回合越後面,加上的噪聲越多。
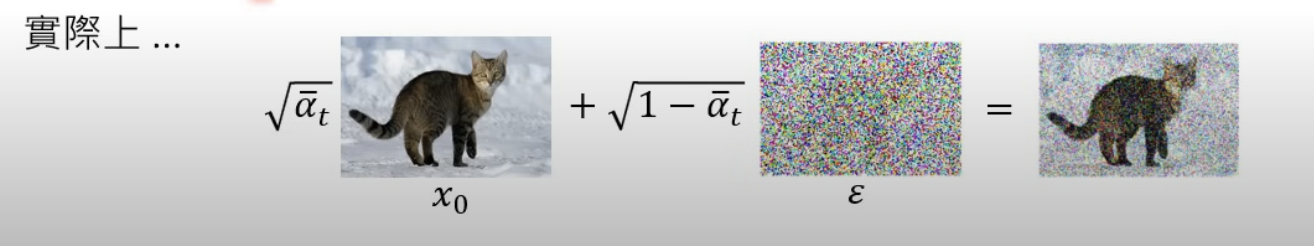
√ᾱ_t x_0 + √(1−ᾱ_t) ε :這邊 ᾱ_t 是根據 Unuiform 出來的 t ,如果 t 值越大,ᾱ_t 越小。 ᾱ_t 越小,代表加上的噪聲比例則越多(右邊乘上的√(1−ᾱ_t))。
目標: 最小化 ,即讓模型輸出的噪聲與實際加入的噪聲越接近越好。
梯度下降: 對模型的損失函數進行梯度下降,更新參數 。利用 MSE 平均平方差損失去算 梯度下降率。
第 6 行:until converged
- 作用: 持續迭代,直到模型訓練收斂。
Algorithm 2: Sampling

第一行 給訂一個 X 大 T 純雜訊圖
- 意義:從標準高斯分佈(均值為 0,方差為 1)中隨機生成一個噪聲樣本作為起始點。
- X 大 T 代表的是 純雜訊圖
第二行 迴圈開始
從純噪聲一路 Sampling 到 生成圖
- 意義:從時間t(最純的噪聲)開始,逐步回溯到 (逐漸去噪直到還原出清晰的數據)。
第三行 噪聲條件
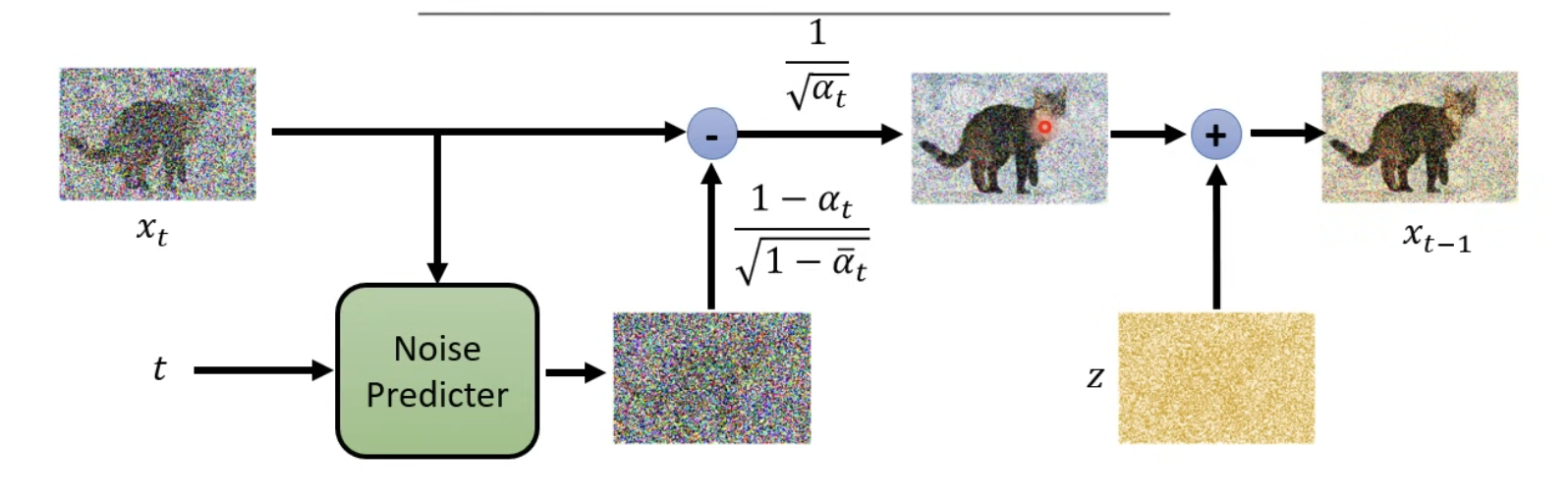
- 意義:在 Sampling 階段,會在做完減去 Noise predictor 後,再加上 z 噪聲(請看第四行)
- 但在 t == 0 時,已經完成 Sampling ,因此不再加上 z 。
第四行
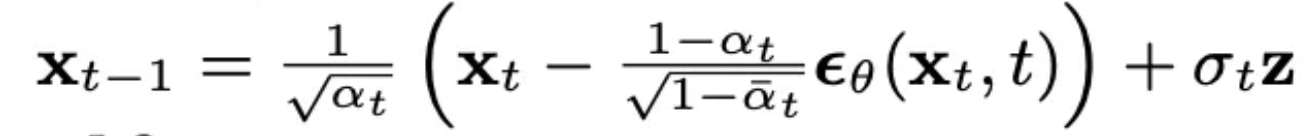
x_{t-1} = (1 / √(a_t)) * (x_t - (1 - a_t) / √(1 - ᾱ_t) * ϵθ(x_t, t)) + σ_t * z
詳見:Sampling 階段 Denoise function 化簡
- 分解理解:
- ϵθ(x_t, t):Noise predicotr 根據當前 t (哪一階段) 生成噪聲
- (x_t - (1 - a_t) / √(1 - ᾱ_t) * ϵθ(x_t, t):從當前數據中減去預測的噪聲部分。
- x_t 代表的則是上一階段的結果,因此 = 右邊是x_{t-1} ,也就是逐步 Sample 到 x0 (clean image)。
- (1 / √(a_t)):(乘號左邊)調整信號幅度,使其回到正確的分佈範圍。
- σ_t * z:添加隨機噪聲 ,模擬反向過程的隨機性。
- 目的:從當前的t還原到上一個t 。
第五行 迴圈結束
第六行 最終輸出
- 意義:當迴圈結束時,輸出最後的結果 ,這就是還原出的清晰數據(如圖像)。
- x0 代表 clean image,因此 return x0。
Maximum Likelihood Estimation
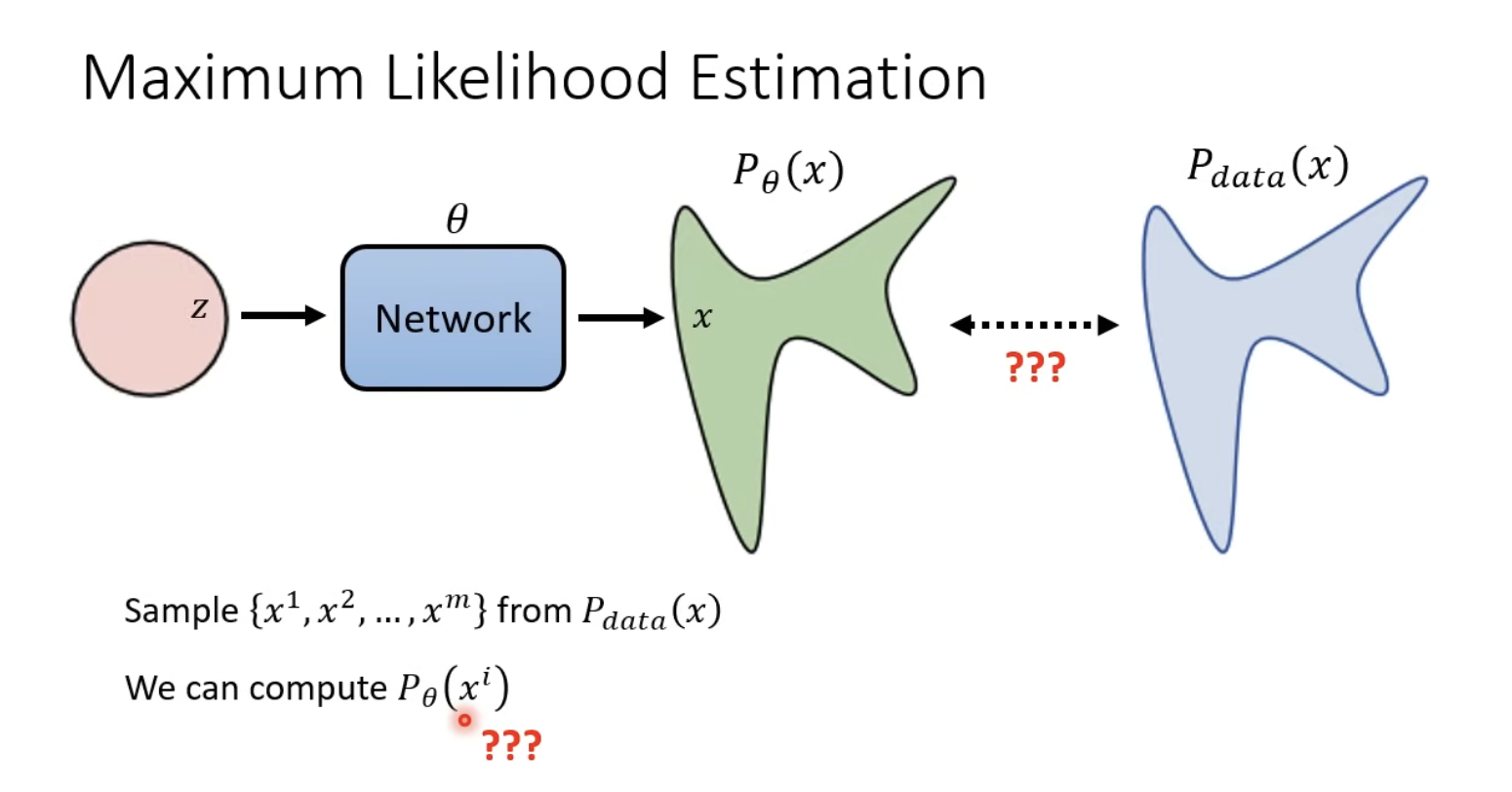
MLE 的目的是為了讓 Pθ 盡可能的接近於 Pdata。
- Pθ(x):model 所 sample 出的 distribution 機率。
- Pdata(x) : 真實世界的 dataset,和 model 的 network 無關。
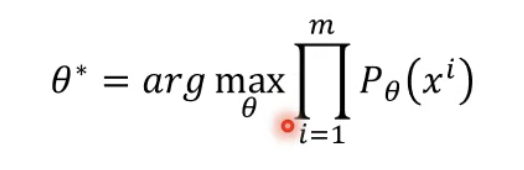
將每一個 sample 出來的 xi 拿 pθ 算出機率 並相乘,竟可能找出最大 θ。
所以我們要找的 θ 就是機率最高的那一個(LHY 在投影片用 θ* 代表)。
network 的目標是學習數據的規律(真實分佈𝑞(𝑥0)q(x0)),然後模擬這些數據的機率,這就是𝑝𝜃(𝑥0)pθ(x0)。它代表模型認為數據𝑥0x0有多「合理」或「可能」。 *from chatgpt
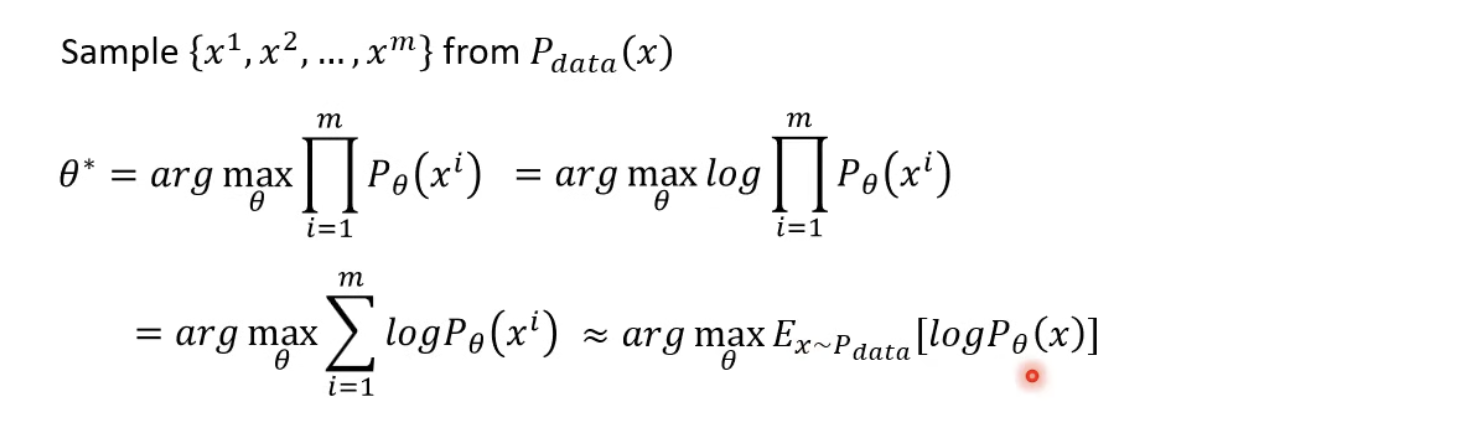
從log 相乘轉換成 相加log ,相加 log 這樣會近似於 從 pdata 取出的 x ,然後 pθ 算出機率 要越大越好。
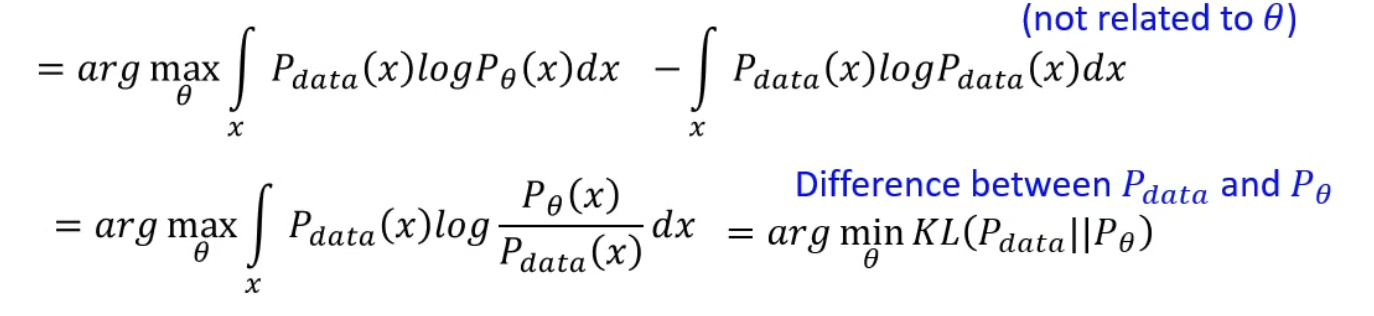
接著從 expectation 轉換為積分,然後可以算出就等同於 KL(Pdata||Pθ) ,所以我們要找 minimun KL。
讓 ptheta 讓 pdata的差異最小。
VAE: Compute pθ
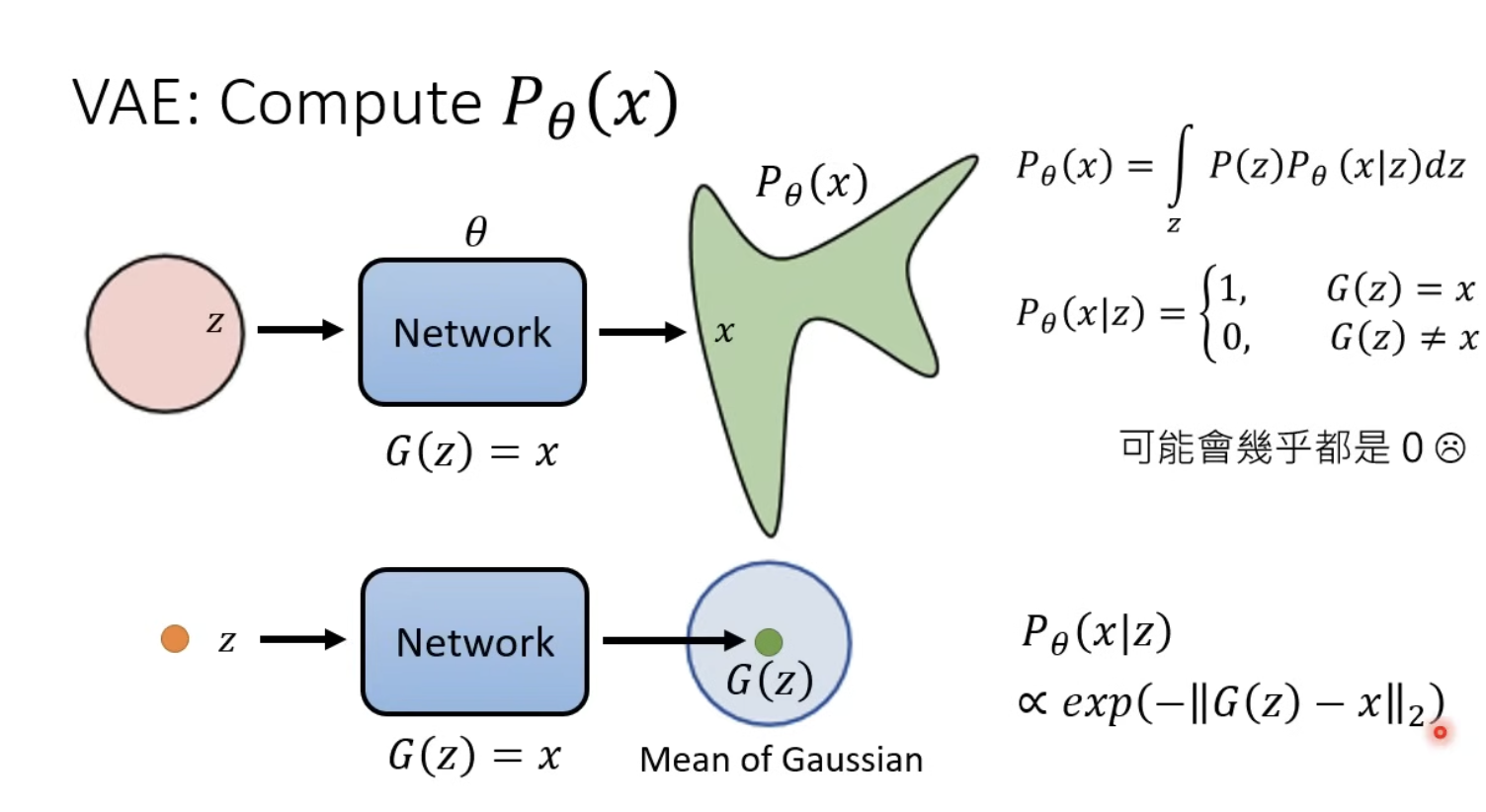
這邊主要是在講說,因為我們不可能去直接看 pθ(x|z) ,因為不可能 sample 出完全一模一樣的圖,這樣會造成 pθ(x|z) = 0。
因此我們是去看 Mean of Gaussian (去看距離,也就是 x 和 G(z)的距離)。
VAE: Lower bound of
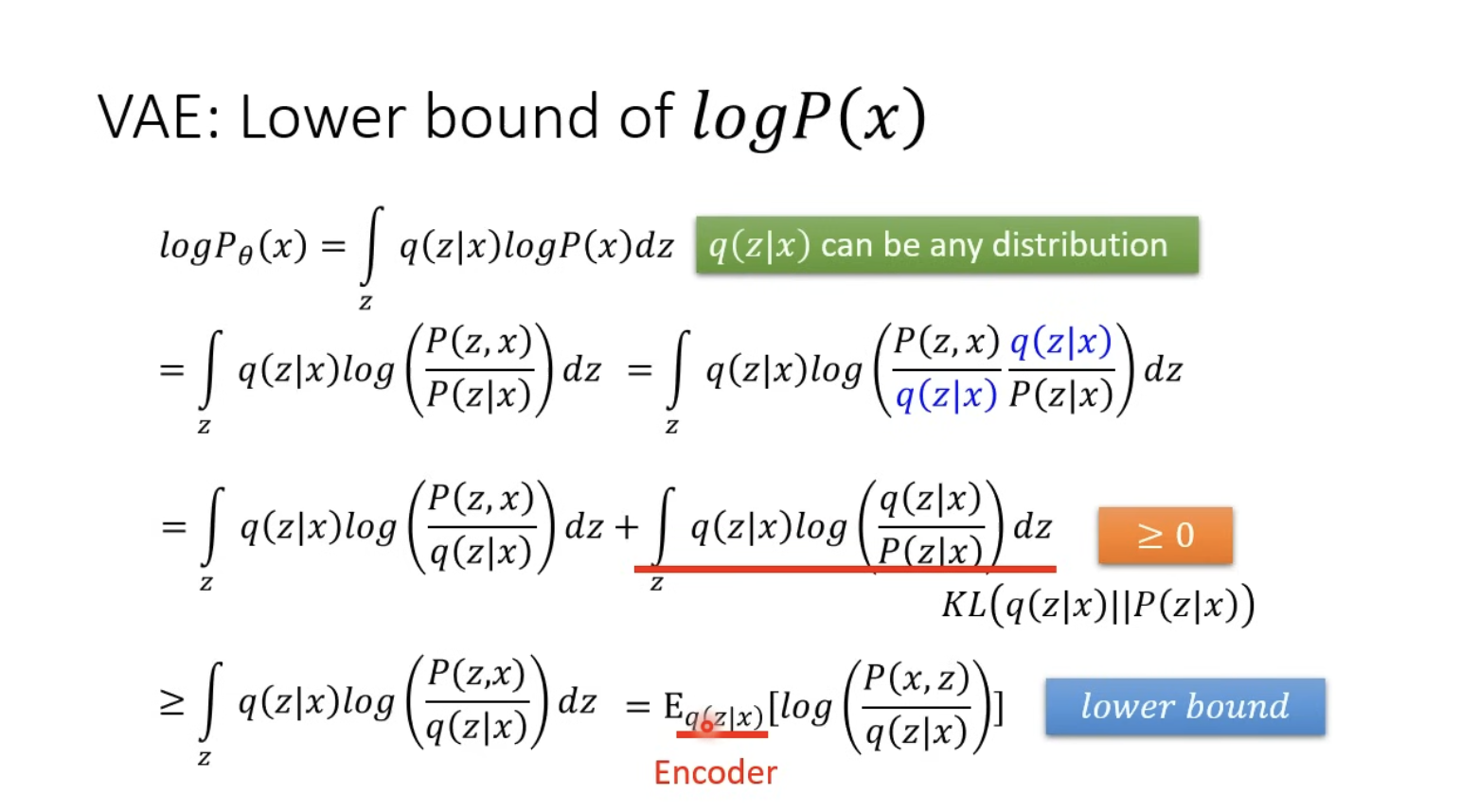
- ≥ 0 是因為 它可以看作 KL divergence 而完全一樣就為0,因此 ≥ 0。
DDPM: Compute pθ(x)
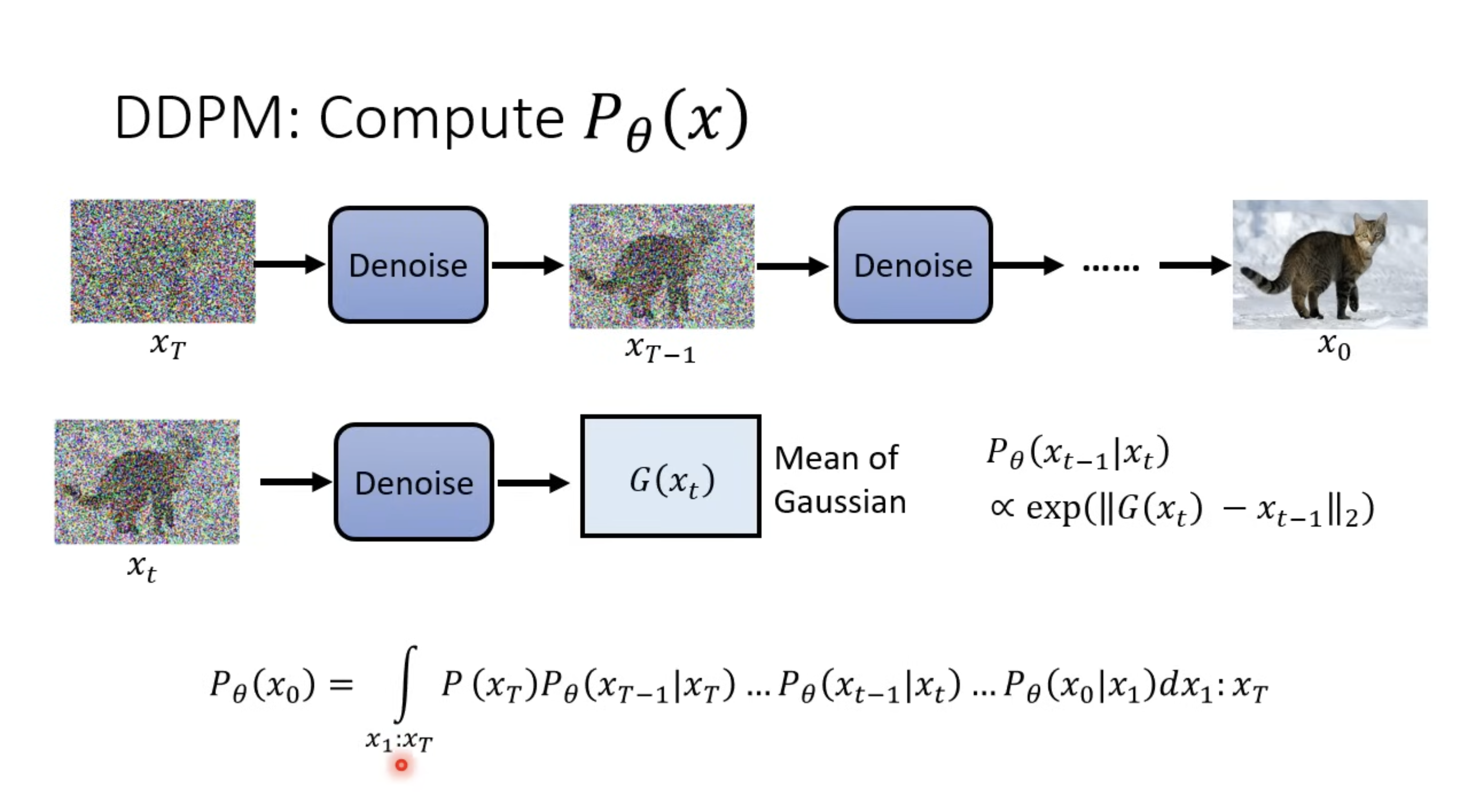
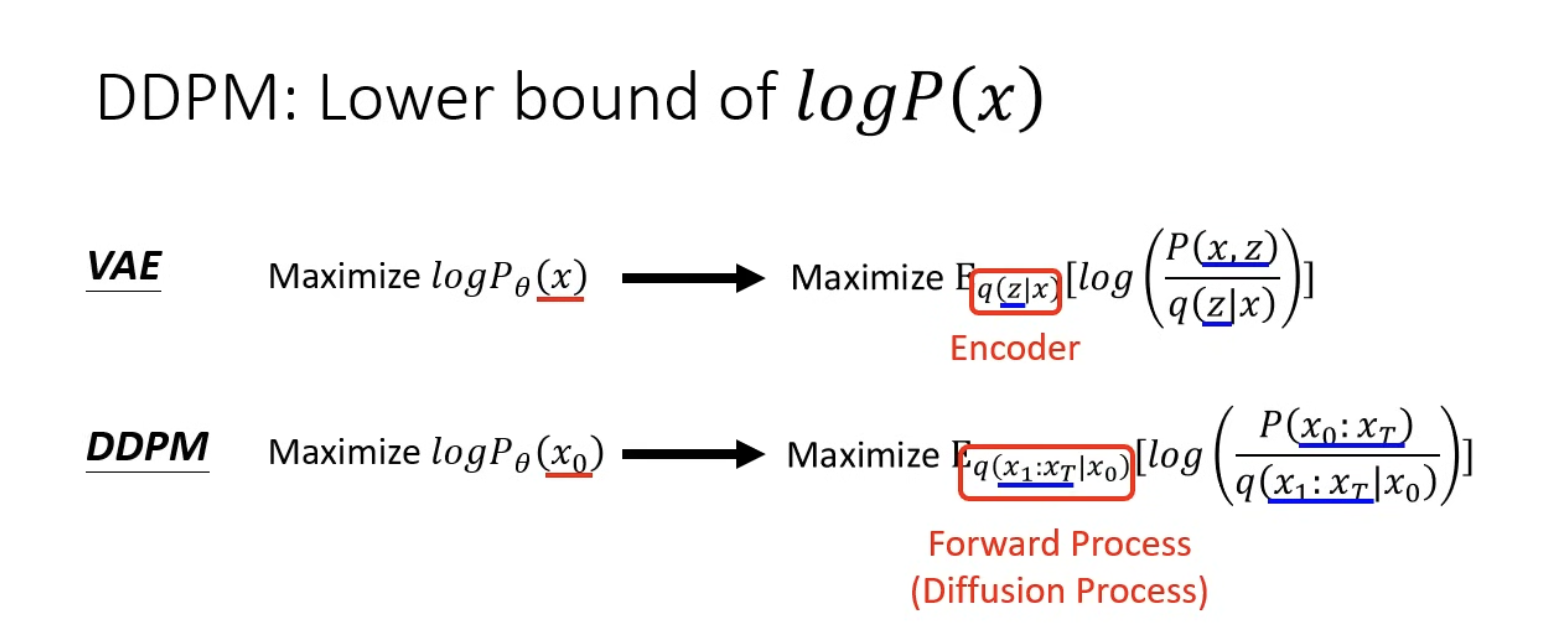
在算 DDPM 時,和 VAE 不同的是, Maximize 期望值時,原先的 Encoder 替換成 Diffusion Process,也就是在加 Noise 的那個階段。
將式子展開後為以下。
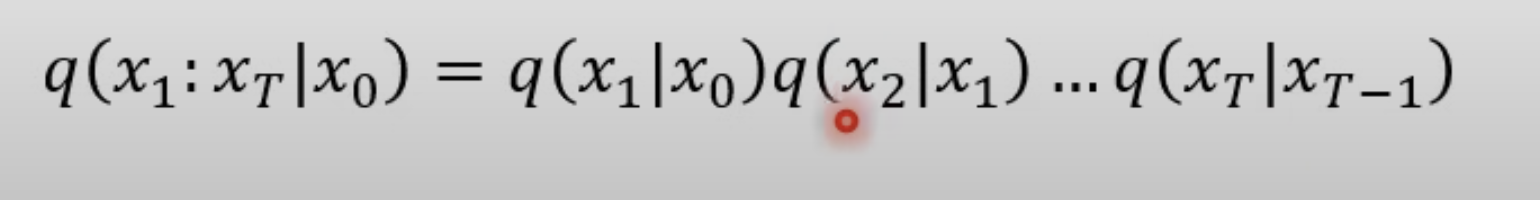
從 x1 一直做到 X 大 T
單個 q(XT | XT-1) 算法
我們首先要先定義一組 β1 ~ βT ,這組數值為自定義的,類似 Learning rate,會根據修改影響 Network。 因為這會影響在每一 t 加上的噪聲
(以下李教授有筆誤,應為 Xt = √1-Bt * Xt-1 + √Bt * noise)
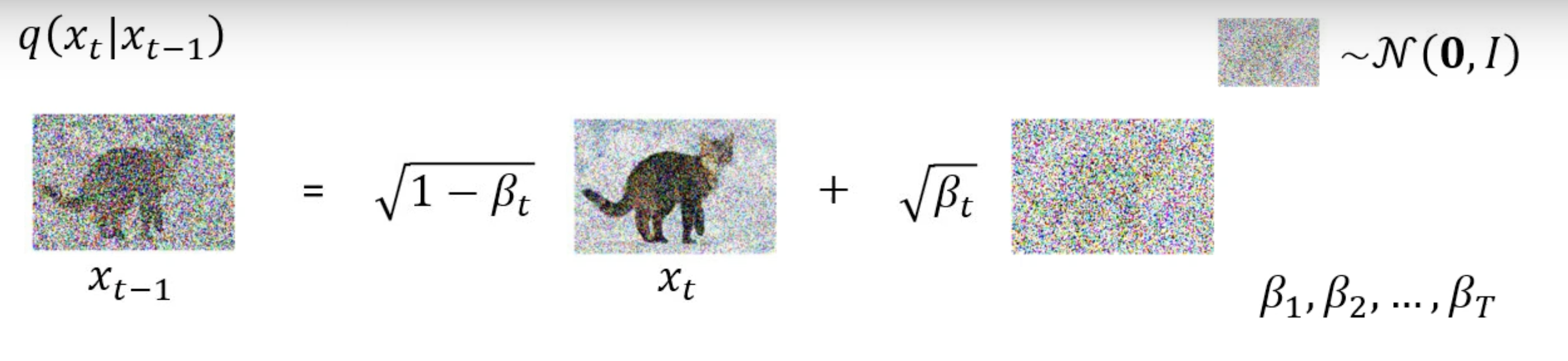
如果要算出 q(XT | X0)
其實是可以不用一次一次去把它算出來(不用一步一步把它+上噪聲)。
從下方可以推導出 q(X2 | X0)
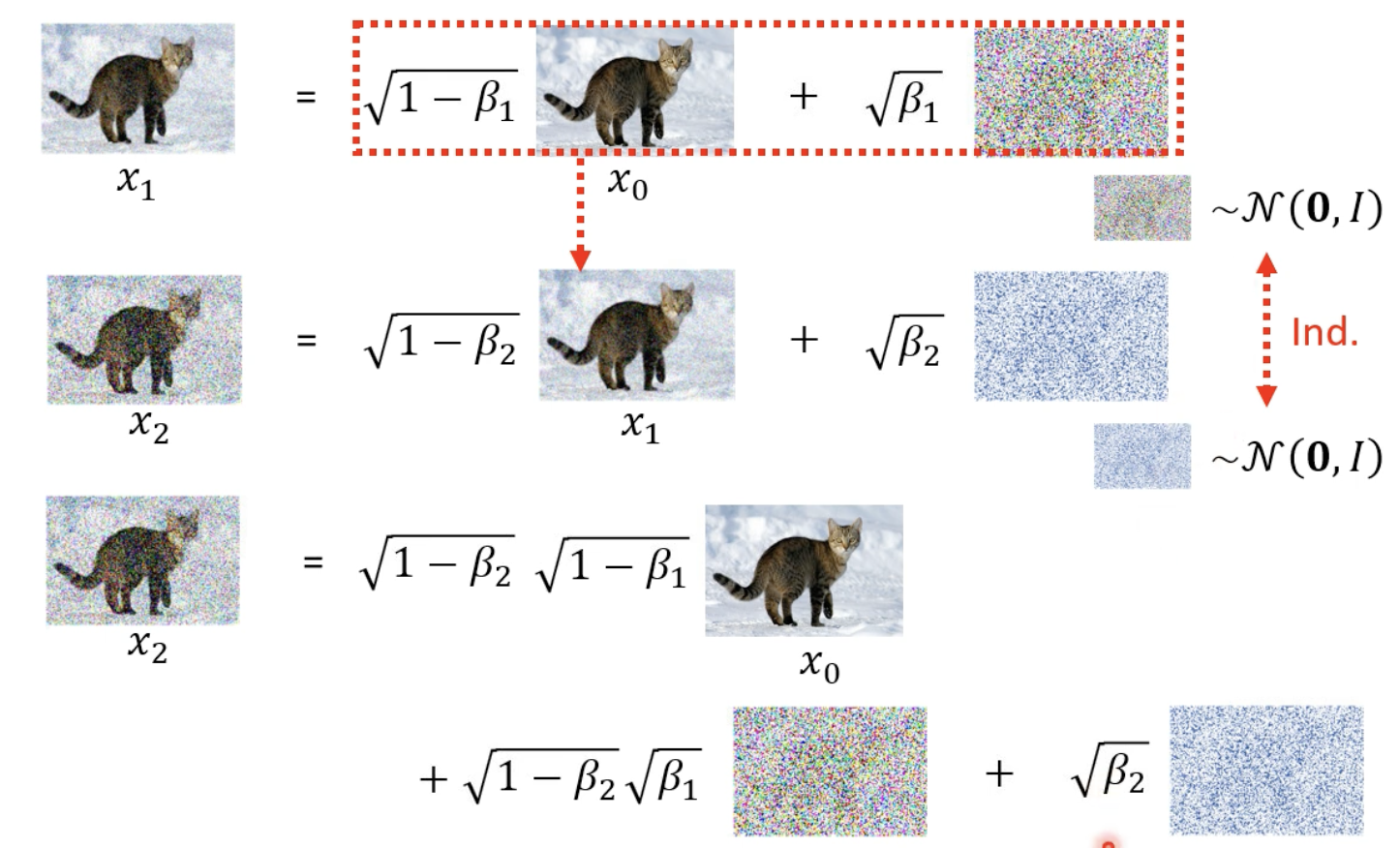



因此 q(Xt | X0) 就可以整理成上圖。
噪聲預測
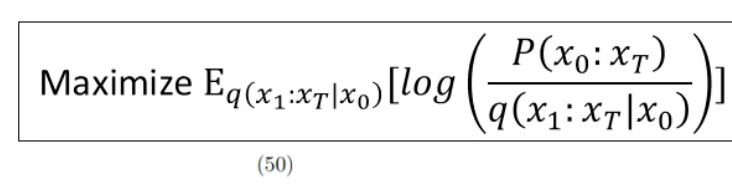
從上圖推導至下圖
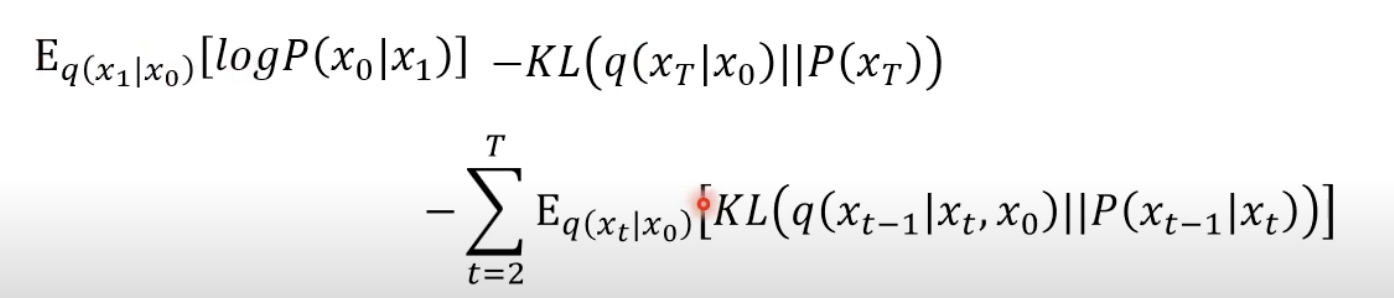
目標就是去最大化,而為了最大化,也就是盡可能地將 KL Divergence 最小化。(看後面的:KL Divergence between 向前 and 向後)
算出 KL Divergence 向前 𝑞 ( 𝑥 𝑡 ∣ 𝑥 𝑡 − 1 ) q(x t ∣x t−1 ) 與向後 𝑃 𝜃 ( 𝑥 𝑡 ∣ 𝑥 𝑡 − 1 ) P θ (x t ∣x t−1 ) 的差異。
$\sum_{t=2}^T E_{q\left(x_t \mid x_0\right)}\left[D_{K L}\left(q\left(x_{t-1} \mid x_t, x_0\right)|| p_\theta\left(x_{t-1} \mid x_t\right)\right]\right.$
算出中間xt-1到xt的分佈 q(Xt-1 | Xt, X0)
前面我們已經講過了,如何算出從 X0 到 Xt,也知道要如何算出 xt-1 到 xt-1 的分佈。
推倒公式如下
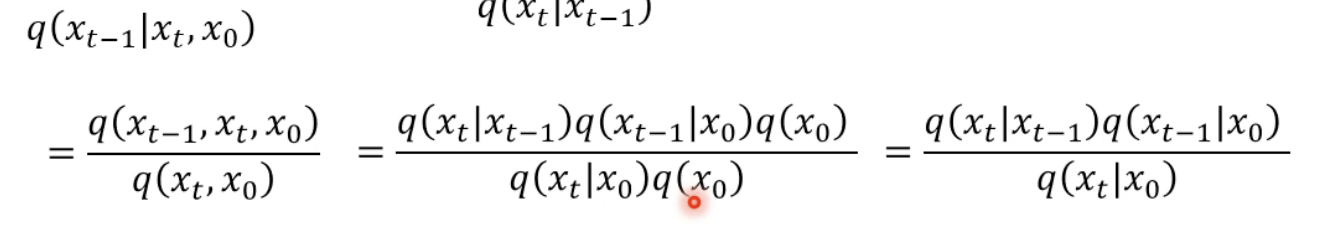
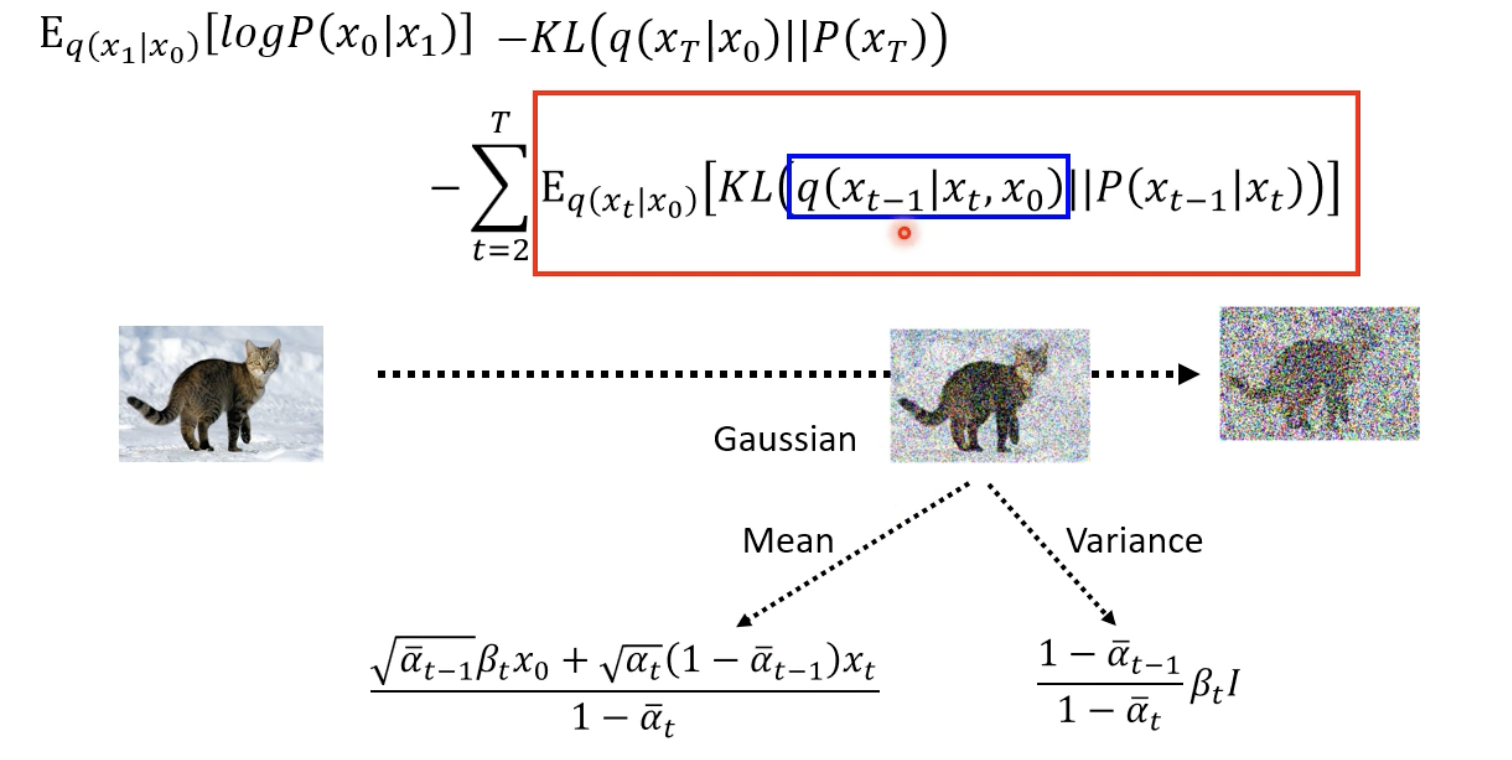
KL Divergence between 向前 and 向後
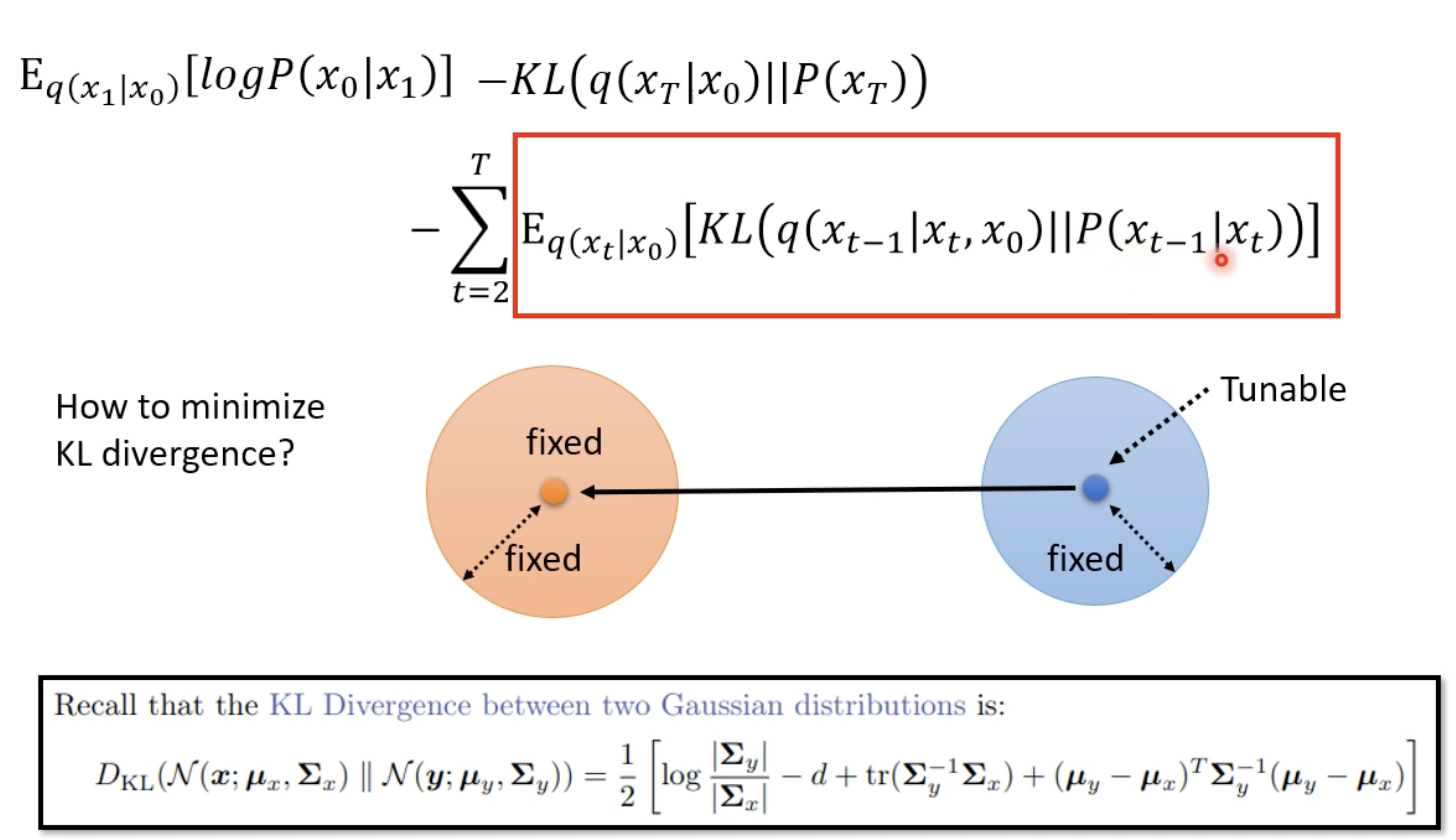
因為向前的 Mean 是不可動的,所以我們唯一可動的就是 P(Xt-1|Xt) 的 Mean ,使兩者離中心點的距離最小,這樣一來,就可以使得 KL Divergence 盡可能的小。
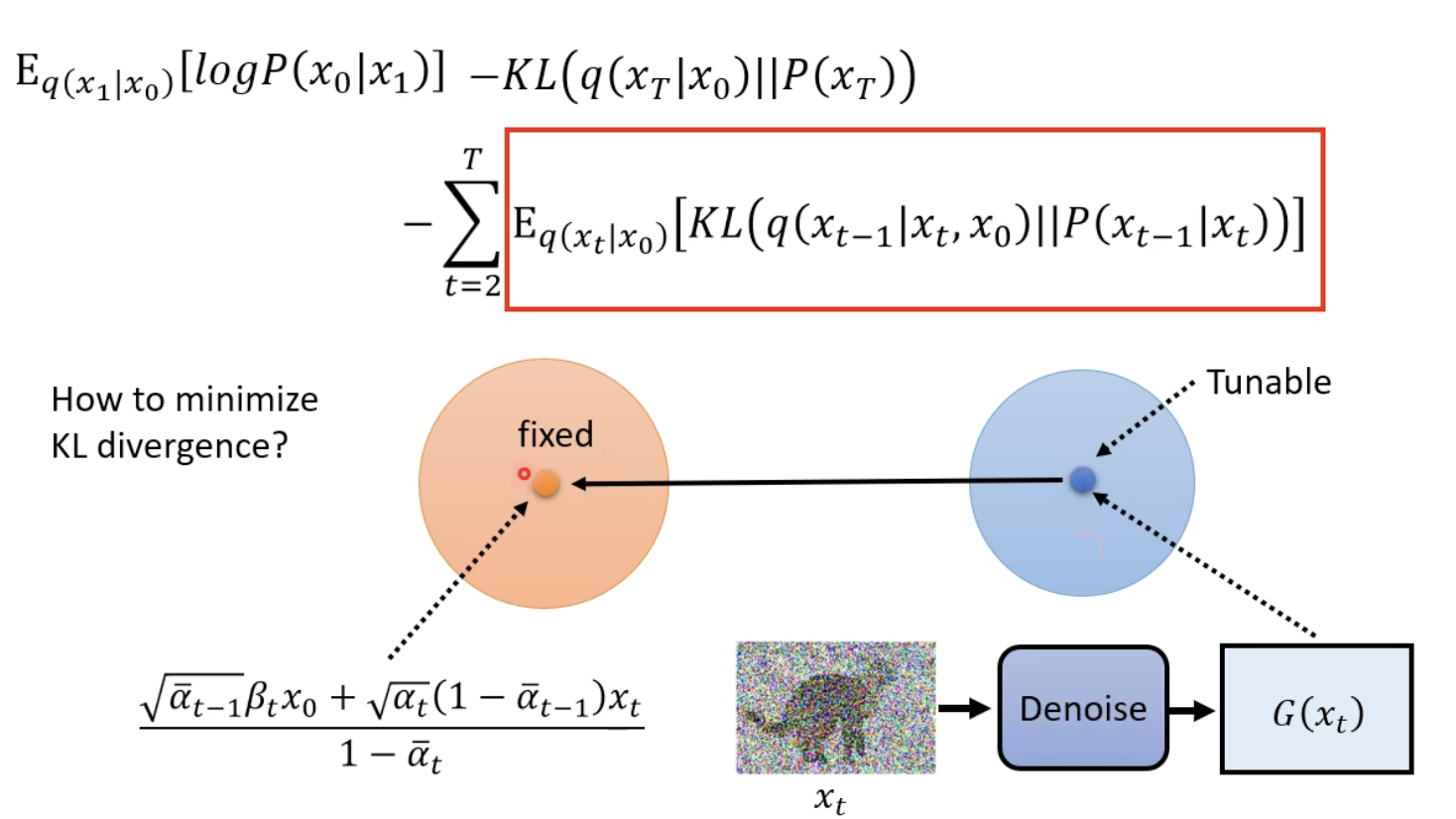
所以說以上在做的事情也就是訓練 denoise function ,使得它們兩者越相近越好。
Sampling 階段 Denoise function 化簡
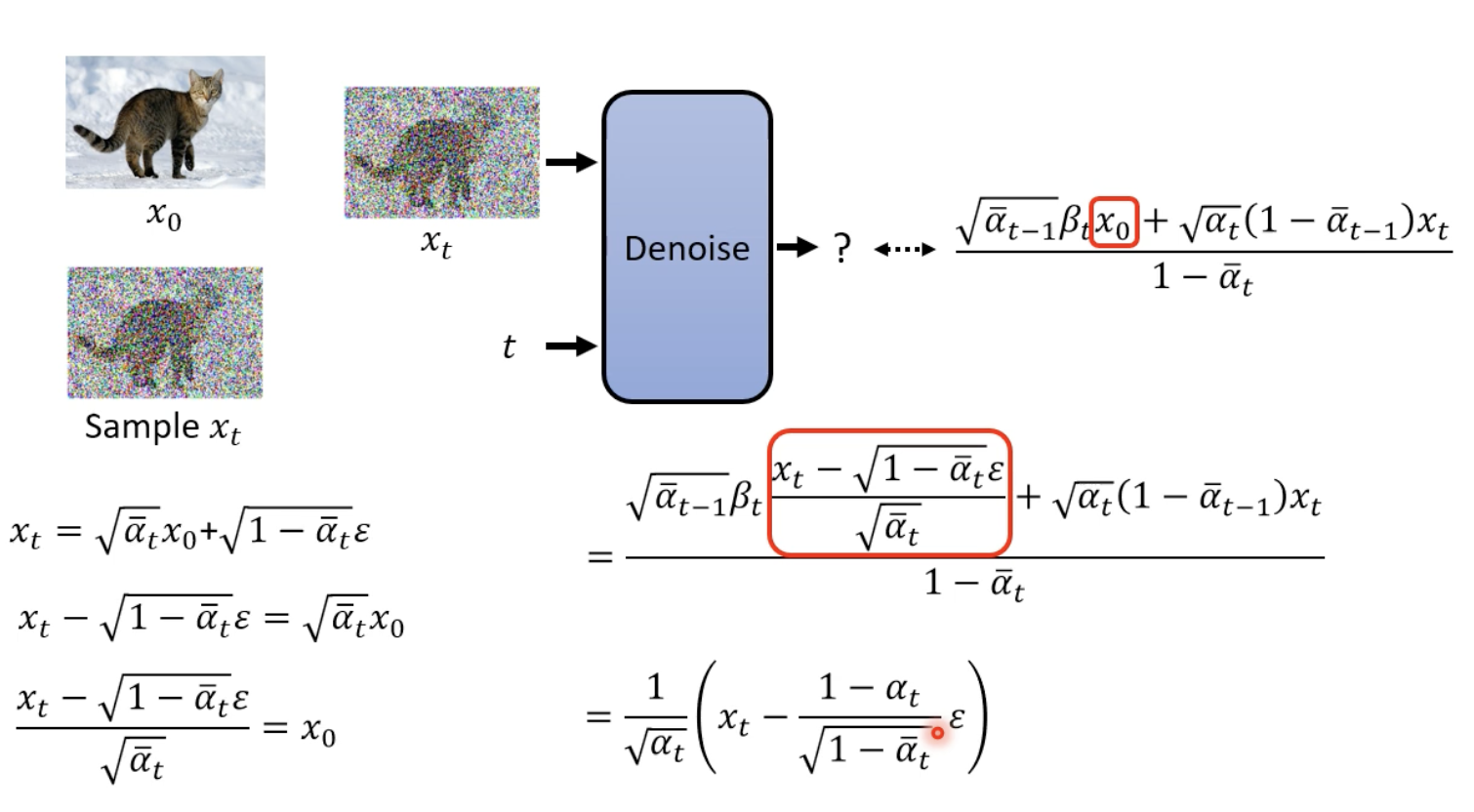
原先右上角的式子的 x0 可以根據我們上面已經寫好關於 x0 和 xt 的關係,在帶回去化簡。
而這邊也就回到 Algorithm Sampling 階段的第四行。
